Entering Financial Calculus

In the realm of technical analysis of the stock market, graphical and candlestick analysis is key to great success as a trader. Millions of traders across the world plot support lines and resistance lines, as well as use uptrends and downtrends to predict the success of stock and determine where they should enter a stock. They analyze moments where the graph inflects, and the rate at which a stock price changes. Creating measures of volatility, true value indexes, and average true range with the aim of better understanding a stock is a commonality amongst traders. But beyond its advantage in trading, what is the mathematical significance and proof of this analysis? How does complex mathematics better our contemporary understanding of the stock market? The concept of slope and graph theory has a strong prevalence in the technical analysis aspect of the financial market. However, calculus allows us to understand this at a greater depth. Calculus benefits us in this context because of how effectively it analyzes rates of change and accumulation. Derivatives – a common technique of calculus – are financial instruments that attain their value from an asset, such as a stock or commodity. The value of the derivative is based on the rate of change of this asset, which can be analyzed using calculus. This allows traders and investors to make predictions about the future behavior of the market and make trades accordingly, based on how quickly the value is changing. Derivatives can be applied to graphs that have already been derived. In the graph, we can see a red line that represents the stock price after removing external value (corporate, dividend, etc.) versus the average closing price of the stock on a third period; the latter of which is similar to the derivative in a sense.

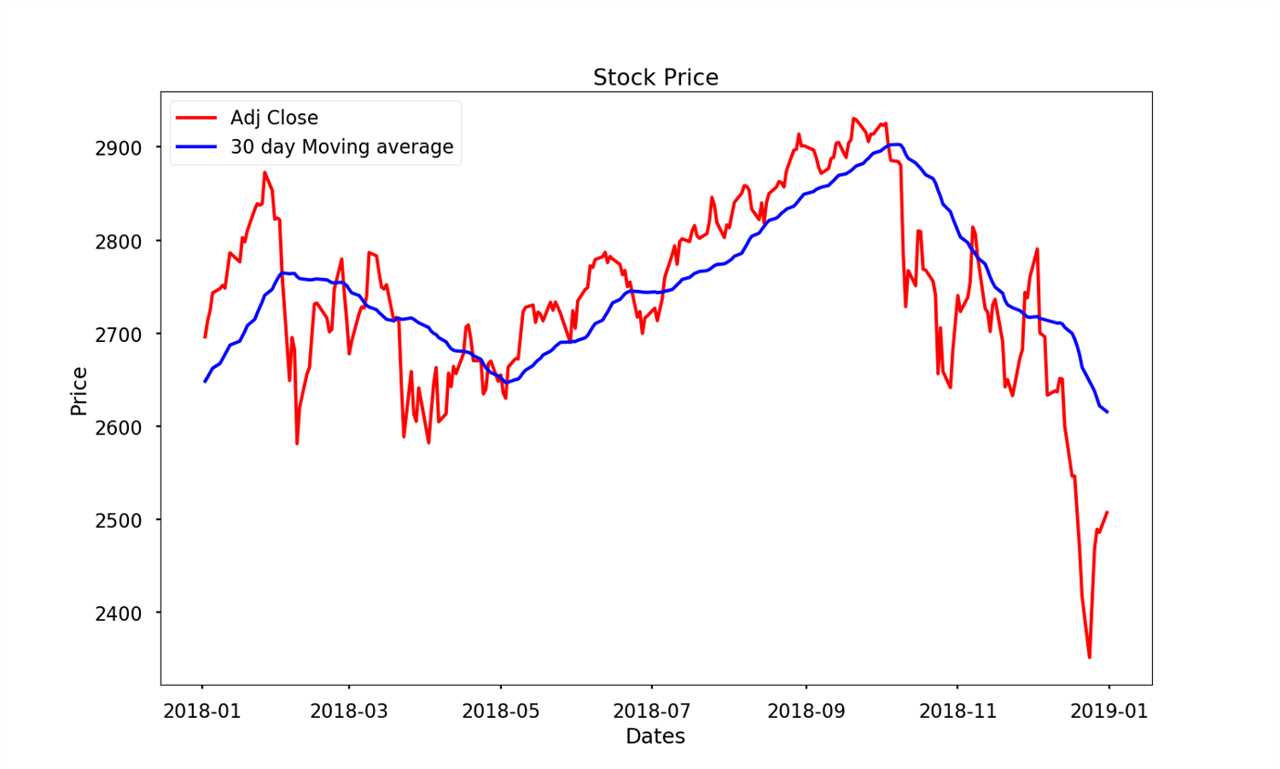
This process is called deriving a function (or in this case the graph of a stock price) to a greater degree. If we derive it twice in total, we are observing the second derivative of the graph, and are effectively observing the rate a rate is changing. The larger the number of times we derive a function, the more we are able to understand why it moves the way it does. It really is interesting how math drives the movements of stock. We can see this used in the model above how the derivative models the path of the stock price. The derivative, although useful, is a simpler tool of calculus, and is only an introduction to what is possible using calculus in the stock market. Using more complex applications of calculus in probability and function behavior can help us view the stock market from an outstanding perspective. Let’s dive into how the calculations that define our success in the market connect to high levels of mathematics and explore how calculus is used in the financial market to make predictions and optimize trading decisions.

Stochastic Calculus: Understanding Probability

Although we can use several metrics and technical analysis techniques, there is not a surefire way of predicting the behavior of a stock with an exact measure. In this sense, there is always an element of randomness that occurs in stock behavior. Although this behavior isn’t truly random and relies heavily on consumer behavior and options, there is a certain extent to which predictive algorithms can be useful. This is where stochastic calculus, the randomness of calculus, comes into play. Before we can understand how this applies to the stock market, it is imperative that we understand the essence of random behavior as a whole. If we were to create a ”random” chart of x and y values, we would get something like this:

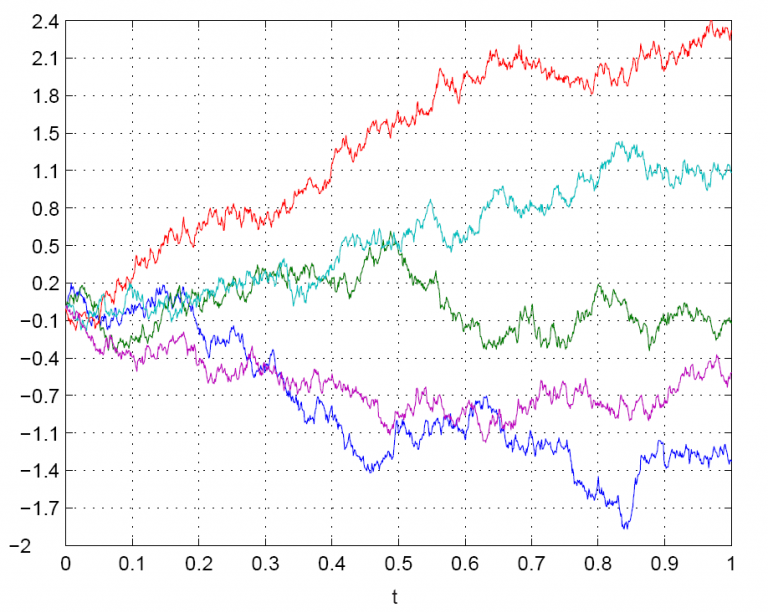
This behavior is known as “Brownian motion”, which can also be displayed as a bell curve with normal distribution.

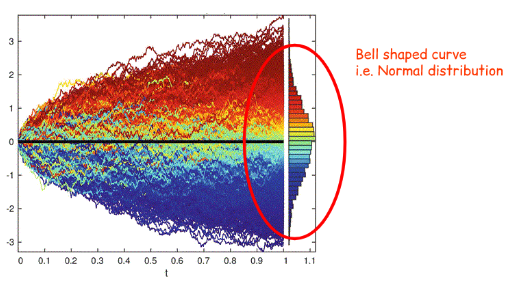
Even though this is considered “random” motion, it is still relatively predictable. This is what is known as normal distribution, where there is an even distribution about the center of the data. As displayed in the graphs above, there are negative values of this chart. In the stock market, negative values are not possible, and therefore, we use geometric brownian motion rather than simple brownian motion (log-normal compared to normal distribution).

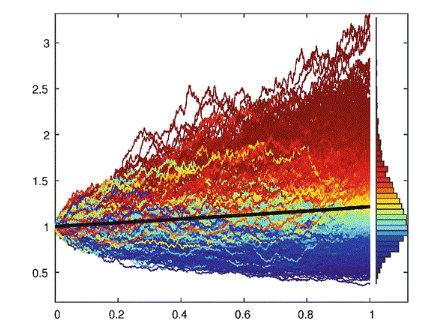
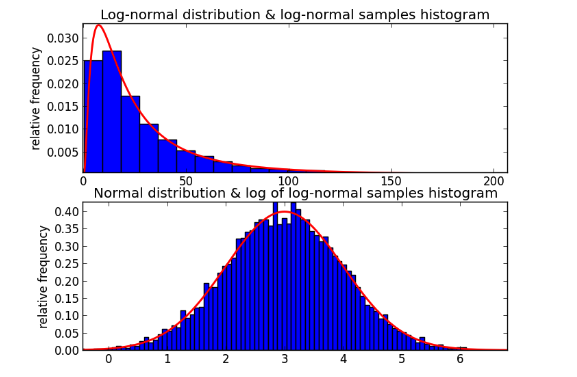
Now that we have a fundamental understanding of randomness, we can use this in the calculus of the stock market. Because in calculus we can only calculate the derivative of a function if it lacks sharp corners and turns, most of the time, we cannot apply this concept to the constantly-changing stock prices of the stock market. Japanese mathematician Kiyoshi Itô derived a formula for the derivative using geometric brownian motion. dSt = tStdt+StdBt, where S refers to stock price. This calculus can simply be explained as “Change in S = Constant A * Current S * change in time + Constant B * Current S * change due to randomness as modeled by GBM … Which means the change in the stock price = current stock price multiplied by some constant value over time + current stock price + change due to randomness multiplied by another constant. That should intuitively make sense as over time, the change of the stock price is based on some overall trend (the Constant A part) and an element of randomness (the Constant B part and randomness part). Constant A and Constant B are usually derived by analyzing historical market data.” Here, randomness serves as the volatility of the stock, which is also defined by independent behavior and principles. Another application of a calculus based theorem applies to option trading. The Black-Scholes equation refers to determining the cost of “hedging” a particular option. “Hedging” an option, here, refers to combining several stocks and allocations to those stocks that will eliminate the risks to pre-existing trades. A full derivation of this equation can be found here, but it generally simplifies to the following.

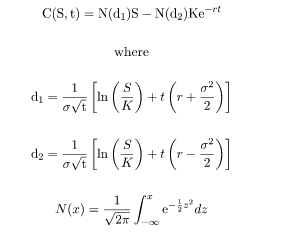
To summarize, calculus is used to define random behaviors in the stock market and provide models and analysis to make more accurate predictions about the future of a stock. Stochastic calculus is a branch of calculus that deals with random behaviors, where in the stock market, prices are unpredictable and fluctuate. Using brownian generalizations and calculus, we can use theorems and equations to understand the randomness and move past it. By using stochastic calculus, analysts can define random behaviors in the stock market and develop models to predict the behavior of stocks.

Algorithmic Trading

Another application of calculus is used to optimize entry and exit points in the stock market. This starts with the premise of the second derivative and concavity. Like the derivative, the second derivative refers to the rate of the rate a function is changing. The simplest way to classify concavity is through concave up and concave down.

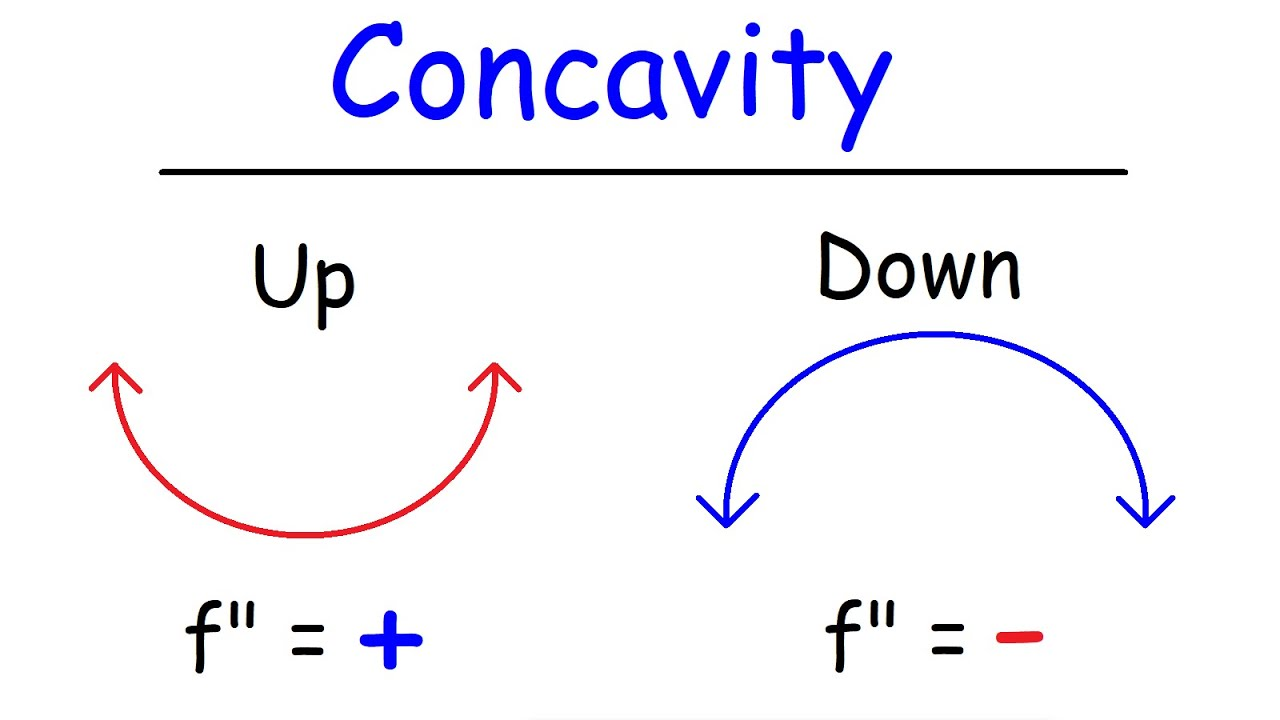
We can observe the points where there is a horizontal tangent in the middle of each of the lines. This is a basic indicator of a stock price in the sense that when the slope of a stock is approaching zero, we can use the premise of concavity to understand stock graphs. This is just an introduction to algorithmic trading, which uses these ideas to a greater level. Advanced market analysts and mathematicians, known as quants, write extensive formulas with calculus and translate it to code. This code is then utilized in the market by computers.

These algorithms use slope and other calculus-based concepts to determine optimal option trades. Quants, or quantitative analysts, use these calculations in their work to optimize trading decisions. Many people have derived their own formulas through calculus and technical analysis to use in their trades, but more meaningfully, many investing corporations at international levels use these formulas along with fundamental analysis to manage their investing. Over recent history, algorithmic trading has maintained a 10% return above the market and allows for rapid selling-buying interactions that outclass human speeds. Although the premise of an algorithmic – almost emotionless – side to trading is appealing in a sense, there are in fact downsides to this process. According to Investopedia, algorithmic trading has been the cause of various mini crashes in the 2000s, as well as making “liquidity, which is created through rapid buy and sell orders, disappear in a moment, eliminating the chance for traders to profit off price changes. It can also lead to instant loss of liquidity. Research has uncovered that algorithmic trading was a major factor in causing a loss of liquidity in currency markets after the Swiss franc discontinued its Euro peg in 2015.” Presenting both effective and negative results, algorithmic trading is another method of extensive calculus in the market.

The Greeks and the Golden Ratio

Used in the powerful methods of algorithmic trading explained above, the Greeks of the market are mathematical calculations used in these formulas that are so integral to their success. These values are always changing and based on whichever stock is being evaluated. The most common Greek is Delta, which refers to rate of change. It is most commonly used regarding volatility in options, where Investopedia best explains an example of its usage: “the delta of a call option has a range between 0 and 1, while the delta of a put option has a range between 0 and -1. For example, assume an investor is long a call option with a delta of 0.50. Therefore, if the underlying stock increases by $1, the option’s price would theoretically increase by 50 cents.” Theta, often associated with Delta, refers to the change between an option’s price and time (also known as time sensitivity). This is mostly based on the metrics known as liquidity and volatility, which refer to how much, how often, and by what margin a stock is changing price. Theta is at a higher value when an option is “in the money” (valuable) and lowers when the opposite occurs. Things that don’t necessarily decrease in value over time, such as a stock, would have a Theta value of zero because the inherent value of a stock is constant. Gamma plays into long-term versus short-term value in options and their Delta. Gamma is the “second derivative”, in a sense, of an option’s Delta. It used to determine how much the Delta of an option fluctuates. Higher Gamma means that Delta will react much more to a change in value of an option and will lower when this reaction is not as severe. As the expiration of an option’s value comes closer, the Gamma value is a lot higher because price changes in a stock are a lot more influential. Other minor Greeks, such as Vega (which is the reaction of an option and the volatility of a stock’s value) and Rho (which describes the change between an option’s value and interest rates), are also used in determining the value of an option, but are not as prevalent. As a whole, best explained by Investopedia, “the Greeks are values that estimate the various risk characteristics of an options position. They tell traders how an option is likely to react to changes in the market, such as a change in the price of the underlying asset. Greeks can be used to judge the riskiness of an investment in that option.”

Conclusion

Calculus plays a significant role in the financial market. From stochastic calculus to algorithmic trading and the Greeks, calculus is used to make predictions and optimize trading decisions. The Golden Ratio is embedded in the stock market and is used to identify trends and make informed decisions. Understanding calculus is essential for anyone looking to succeed in the financial market.

---------------------------

By: Sanjay Mukhyala
Title: Calculus In The Stock Market
Sourced From: streetfins.com/calculus-in-the-stock-market/
Published Date: Wed, 15 Mar 2023 04:28:24 +0000

Read More